二次関数の問題を解くときに必要になるのが、二次関数の頂点座標です。
二次関数の頂点と軸
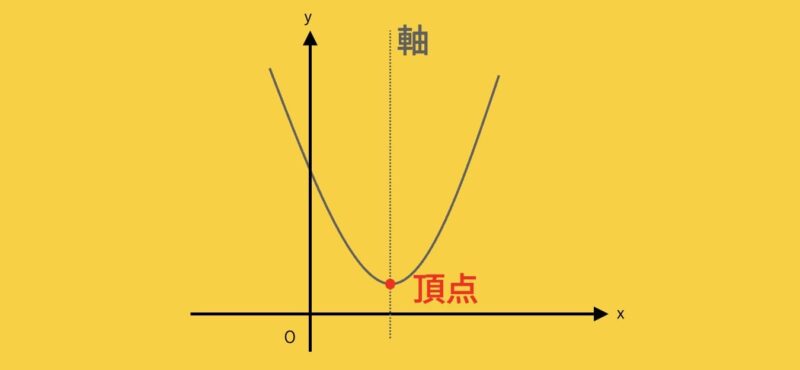
今回はこの頂点と軸の求め方を解説していきます!
二次関数の式の形
今回解説する二次関数の式のパターンは2つです。
- \(y=a(x-b)^2+c\)
- \(y=ax^2+bx+c\)
この2パターンです。
どちらの式も2次関数の問題では出てきます。
ですが、問題を解くときには\(y=a(x-b)^2+c\)の形に変形して解く場合が多いです。
そのため、まずは\(y=a(x-b)^2+c\)の形を解説していきましょう。
そして、\(y=ax^2+bx+c\)を解説していきます。
頂点座標(1)|\(y=a(x-b)^2+c\)
まずは、\(y=a(x-b)^2+c\)の場合の頂点座標と軸の求め方を説明します。
頂点座標の求め方
頂点座標とは、文字通り二次関数の頂点の座標です。
\(y=a(x-b)^2+c\)のとき、頂点座標は\((b,\ c)\)という決まりがあります。
文字だけで出しても理解が難しいと思うので、もう少し具体例を見てみましょう。
頂点座標の具体例
\(y=a(x-3)^2+4\)
頂点座標:\((3,\ 4)\)
\(y=a(x-2)^2-5\)
頂点座標:\((2,\ -5)\)
\(y=a(x+1)^2+6\)
頂点座標:\((-1,\ 6)\)
\(y=a(x+\displaystyle \frac{1}{4})^2+\displaystyle \frac{2}{5}\)
頂点座標:\((-\displaystyle \frac{1}{4}\ \displaystyle \frac{2}{5})\)
と言った具合です。
軸の求め方
軸は頂点を通る\(y\)軸に並行な直線です。
二次関数の中心を通る線と思っておけばいいでしょう。
軸は頂点を通っているため、頂点座標の\(x\)の値が軸の方程式となるわけです。
\(y=a(x-b)^2+c\)のとき、頂点座標は\((b,\ c)\)なので、軸は\(x=b\)と書きます。
こちらも具体例を見ていきましょう。
軸の具体例
\(y=a(x-3)^2+4\)
軸:\(x=3\)
\(y=a(x-2)^2-5\)
軸:\(x=2\)
\(y=a(x+1)^2+6\)
軸:\(x=-1\)
\(y=a(x+\displaystyle \frac{1}{4})^2+\displaystyle \frac{2}{5}\)
軸:\(x=-\displaystyle \frac{1}{4}\)
となるのです。
\(y=ax^2+bx+c\)の場合
続いて、\(y=ax^2+bx+c\)の頂点座標と軸の求め方を見ていきましょう。
求め方は2つあります。
頂点座標と軸の求め方
- 平方完成で\(y=a(x-b)^2+c\)の形に変形する
- 公式を使って求める
1つ目は、平方完成で\(y=a(x-b)^2+c\)の形に変形する方法です。
\(y=a(x-b)^2+c\)の形に変形できれば、頂点座標は\((b,\ c)\)なので簡単に求めることができます。
しかし、平方完成は少しテクニックが必要な計算のため、ここでは公式で求める方法を推奨します。

では、公式での求め方を解説していきます。
\ おすすめの参考書! /
頂点座標と軸の公式
頂点座標と軸の公式
二次関数\(y=ax^2+bx+c\)において、
頂点座標 : \(\left( -\displaystyle \frac{b}{2a},\ \displaystyle \frac{-b^2+4ac}{4a}\right)\)
軸の方程式:\(x=-\displaystyle \frac{b}{2a}\)
となります。
詳しい証明は後ほど紹介するとして、具体例を見ていきましょう。
公式の具体例
【例題】
\(y=2x^2+3x-5\)のとき、二次関数の頂点座標と軸の方程式を求めよ。
【解答】
頂点座標は公式より、
\(\left( -\displaystyle \frac{b}{2a},\ \displaystyle \frac{-b^2+4ac}{4a}\right)\)
問題の二次関数は、\(a=2,\ b=3,\ c=-5\)であるから、
頂点座標:
\(\left( -\displaystyle \frac{3}{2\cdot 2},\ \displaystyle \frac{-(3)^2+4\cdot 2\cdot (-5)}{4\cdot 2}\right)\)
\(=\left( -\displaystyle \frac{3}{4},\ -\displaystyle \frac{49}{8}\right)\)
軸の方程式:
頂点座標より、\(x=-\displaystyle \frac{3}{4}\)

平方完成ができれば解ける問題です。しかし平方完成は計算に時間がかかるため、公式を覚えておいて損はないでしょう。検算もできますからね!
頂点座標と軸の公式|証明
では、公式を証明していきましょう!
公式の証明は平方完成を使います。
(再掲)頂点座標と軸の公式
二次関数\(y=ax^2+bx+c\)において、
頂点座標 : \(\left( -\displaystyle \frac{b}{2a},\ \displaystyle \frac{-b^2+4ac}{4a}\right)\)
軸の方程式:\(x=-\displaystyle \frac{b}{2a}\)
頂点座標と軸の公式|証明
\begin{eqnarray}
y&=&ax^2+bx+c \\
&=& a(x^2+\displaystyle \frac{b}{a}x)+c\\\\
&=& a(x+\displaystyle \frac{b}{2a})^2-(\displaystyle \frac{b}{2a})^2-c\\\\
&=&a(x+\displaystyle \frac{b}{2a})^2-(\displaystyle \frac{b^2}{4a^2}+c)\\\\
&=&a(x+\displaystyle \frac{b}{2a})^2-(\displaystyle \frac{b^2-4a^2c}{4a^2})\\\\
&=&a(x+\displaystyle \frac{b}{2a})^2+\displaystyle \frac{-b^2+4a^2c}{4a^2}
\end{eqnarray}
このように変形できる。
\(y=a(x-b)^2+c\)の頂点座標は\((b,\ c)\)であるため、
\(y=ax^2+bx+c\)の頂点座標は、 \(\left( -\displaystyle \frac{b}{2a},\ \displaystyle \frac{-b^2+4ac}{4a}\right)\)である。
軸の方程式は\(x=-\displaystyle \frac{b}{2a}\)となる

微分を使えばもっと簡単にできるから、番外編として最後に紹介します!
番外編|微分で求める頂点座標
微分が使えるなら、知っておきたい頂点を求める方法があります。
微分は関数の傾きを求める計算です。
そして、二次関数の頂点では絶対に傾きが\(0\)になることを利用した方法です。
実際にやってみましょう。
【例題】
\(y=2x^2-8x+5\)の頂点座標を求めなさい。
このとき\(y\)を\(x\)で微分すると、この関数の傾きを出すことができます。
\(y’=4x-8\)と言った具合です。
説明した通り、二次関数の頂点は傾きが\(0\)になります。
逆に言えば、\(y’=0\)の点が頂点となるのです。
【解答】
\(y’=4x-8\)なので、\(x=2\)のとき\(y’=0\)となる。
\(y=2x^2-8x+5\)で\(x=2\)を代入すると、
\(y=2\cdot 2^2-8\cdot2+5=-3\)となる。
以上より、頂点座標は\((2,\ -3\)である。
もちろん頂点座標と軸の公式の証明にも使えます。
頂点座標と軸の公式|証明(微分編)
\(y=ax^2+bx+c\)のとき、\(y’=2ax+b\)である。
\(x=-\displaystyle \frac{b}{2a}\)のとき、\(y’=0\)となる。
また、\(x=-\displaystyle \frac{b}{2a}\)を\(y\)に代入すると、
\begin{eqnarray}
y &=&a \left( -\displaystyle \frac{b}{2a} \right)^2+b\left( -\displaystyle \frac{b}{2a}\right)+c \\\\
&=&\displaystyle \frac{b^2}{4a}-\displaystyle \frac{b^2}{2a}+c\\\\
&=&\displaystyle \frac{b^2-2b^2+4ac}{4a}\\\\
&=& \displaystyle \frac{-b^2+4ac}{4a}
\end{eqnarray}
以上より、頂点座標は \(\left( -\displaystyle \frac{b}{2a},\ \displaystyle \frac{-b^2+4ac}{4a}\right)\)
となります。
\ おすすめの参考書! /
まとめ
二次関数の頂点座標と軸のまとめです。
- \(y=a(x-b)^2+c\)の頂点座標は\((b,\ c)\)
- \(y=ax^2+bx+c\)の場合は公式を使う
- 公式の証明は平方完成か微分を使うとできる
となります!


コメント