指数関数と対数関数の公式は数が多く、利用頻度も高いです。ここでは、重要な公式を一覧でまとめました。
利用例も載せているので、公式を忘れてしまったとき、公式の使い方を確認したいとき、問題を解くとき、ぜひ参考にしてください。
指数関数の公式一覧
指数とは
指数とは、$a$を$n$個かけたものを$a^n$ ($a$の$n$乗)とかき、$n$を$a$の指数といい、$a$を底といいます。 また、$a^1$, $a^2$, $a^3$,…を$a$の累乗といいます。
指数についての定義や法則について確認しよう
整数の指数
0や負の整数の指数
$a\neq0$で、$n$が整数のとき $a^0=1$, $a^{-n}=\frac{1}{a^n}$ 特に $a^{-1}=\frac{1}{a}$
使用例
$2^0=1$, $2^{-2}=\frac{1}{2^2}=\frac{1}{4}$, $2^{-1}=\frac{1}{2}$
指数法則(指数が整数)
$a\neq0$, $b\neq0$で、$m$, $n$が整数のとき
- $a^ma^n=a^{m+n}$
- $(a^m)^n=a^{mn}$
- $(ab)^n=a^nb^n$
- $\frac{a^m}{a^n}=a^m\div a^n=a^{m-n}$
- $\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}$
使用例
- $a^2a^3=a^{2+3}=a^5$
- $(a^2)^3=a^{2\times3}=a^6$
- $(2a)^2=2^2a^2=4a^2$
- $\frac{a^5}{a^2}=a^{5-2}=a^3$
- $\left(\frac{2}{3}\right)^2=\frac{2^2}{3^2}=\frac{4}{9}$
累乗根
累乗根とは、nを正の整数とするとき、n乗してaになる数をaのn乗根といい、$\sqrt[n]{a} (a>0とする)$と表します。
3乗して5になる数は$\sqrt[3]{5}$(3乗根5)と表します。
2乗根、3乗根、4乗根、・・・をまとめて累乗根といいます。 (特に2乗根は平方根、3乗根は立方根ともいいます)
累乗根の性質
$a>0\ ,\ b>0でm,n,p$が正の整数のとき
- $\left(\sqrt[n]{a}\right)^n=a$
- $\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}$
- $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
- $\left(\sqrt[n]{a}\right)^m=\sqrt[n]{a^m}$
- $\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}$
使用例
- $\sqrt[3]{27}=\sqrt[3]{3^3}=3$
- $\sqrt[3]{2}\sqrt[3]{3}=\sqrt[3]{2\times3}=\sqrt[3]{6}$
- $\frac{\sqrt[4]{32}}{\sqrt[4]{2}}=\sqrt[4]{\frac{32}{2}}=\sqrt[4]{16}=\sqrt[4]{2^4}=2$
- $\left(\sqrt[3]{4}\right)^2=\sqrt[3]{4^2}=\sqrt[3]{16}$
- $\sqrt[4]{\sqrt[3]{7}}=\sqrt[4\times3]{7}=\sqrt[12]{7}$
有理数の指数
$a>0$で、$m,n$が正の整数、$r$が正の有理数であるとき、$a^\frac{m}{n}=\sqrt[n]{a^m}=\left(\sqrt[n]{a}\right)^m$、特に$a^\frac{1}{n}=\sqrt[n]{a},\ a^{-r}=\frac{1}{a^r}$
使用例
${27}^\frac{2}{3}=\sqrt[3]{{27}^2}=\sqrt[3]{3^{3\times2}}=\left(\sqrt[3]{3^3}\right)^2=3^2=9 2^\frac{1}{3}=\sqrt[3]{2},\ 2^{-3}=\frac{1}{2^3}=\frac{1}{8}$
指数法則 (指数が有理数)
$a>0$, $b>0$で、$r,s$を有理数とする。
$a^ra^s=a^{r+s}$
$\frac{a^r}{a^s}=a^r\div a^s=a^{r-s}$
$\left(a^r\right)^s=a^{rs}$
$\left(ab\right)^r=a^rb^r$
$\left(\frac{a}{b}\right)^r=\frac{a^r}{b^r}$
※参考記事
[数2]指数法則と指数の拡張
使用例
- $3^\frac{2}{3}\times3^\frac{4}{3}=3^{\frac{2}{3}+\frac{4}{3}}=3^2=9$
- $5^\frac{3}{4}\div5^{-\frac{5}{4}}=5^{\frac{3}{4}-\left(-\frac{5}{4}\right)}=5^\frac{8}{4}=5^2=25$
- $\left(3^\frac{3}{2}\right)^\frac{4}{3}=3^{\frac{3}{2}\times\frac{4}{3}}=3^2=9$
- $\left(4x^2\right)^\frac{1}{2}=2^{2\times\frac{1}{2}}x^{2\times\frac{1}{2}}=2x$
- $\left(\frac{a^9}{27}\right)^\frac{2}{3}=\frac{a^{9\times\frac{2}{3}}}{3^{3\times\frac{2}{3}}}=\frac{a^6}{3^2}=\frac{a^6}{9}$
指数関数のグラフ
指数関数$y=a^x$について、$a>1$のときグラフは$(0,1)$を通り右上がりです。
$0<a<1$のときグラフは$(0,1)$を通り右下がりです。

※参考記事
[数2]指数関数のグラフの書き方、マイナスの場合、平行移動を解説
対数関数の公式一覧
対数とは
対数とは、$a>0$ ,$a\neq 1$ とするとき、正の整数$M$に対して、$a^p=M$となる実数$p$がただ1つ決まります。
この$p$を$\log_a{M}$と表し$a$を底(てい)とする$M$の対数といいます。 $M$をこの対数の真数といいます。
指数と対数の関係
$M=a^p \Leftrightarrow \log_a{M}=p$ $\log_a{M}$は$a$を何乗したら$M$になるのか?という指数の値を求める式です。
使用例
$16=2^4$ であるから $\log_2{16}=4$
対数の性質
$a>0$,$b>0$,$c>0$,$a\neq 1$,$b\neq 1$,$c\neq 1$,$M>0$,$N>0$,$k$は実数のとき
- $\log_a{a}=1$,$\log_a{1}=0$,$\log_a{\frac{1}{a}=-1}$
- $\log_a{MN}=\log_a{M}+\log_a{N}$
- $\log_a{\frac{M}{N}=\log_a{M}-\log_a{N}}$
- $\log_a{M^k}=k\log_a{M}$
- $\log_a{b}=\frac{\log_c{b}}{\log_c{a}}$ (底の変換公式)
※参考記事
[数2]底の交換公式の使い方と証明
使用例
- $\log_2{2}=1$,$\log_3{1}=0$, $\log_3{\frac{1}{3}}=\log_3{3^{-1}}=-1$
- $\log_8{2}+\log_8{4}=\log_8{2\times4}=\log_8{8}=1$
- $\log_5{100}-\log_5{4}=\log_5{\frac{100}{4}}=\log_5{25}=\log_5{5^2}=2$
- $\log_3{16=\log_3{2^4}=4\log_3{2}}$
- $\log_2{5}\bullet\log_5{4}=\log_2{5}\bullet\frac{\log_2{4}}{\log_2{5}}=\log_2{4}=\log_2{2^2}=2$
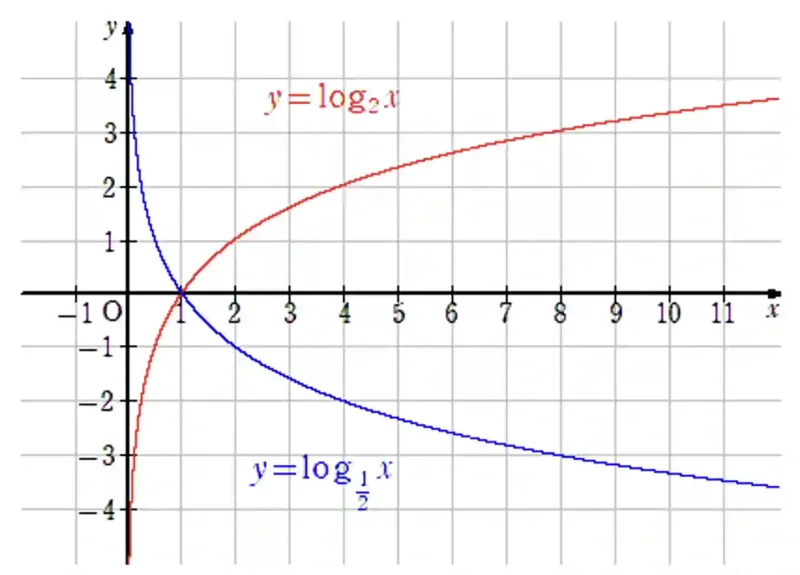
対数関数のグラフ
対数関数$y=\log_a{x}$のグラフは$y=a^x$のグラフと直線$y=x$のグラフに関して対称です。

$y=\log_a{x}$のグラフと$y=\log_{\frac{1}{a}{x}}$のグラフは、x軸に関して対称です。

コメント