[数3]tan 0度が0になる理由を解説

三角関数のtan(タンジェント)についての解説です。
y=tanθとすると、θとyには下記の表の関係があります。

θ	0°	30°	45°	60°	90°
y	0	\(\displaystyle \frac{1}{\sqrt{3}}\)	1	\(\sqrt{3}\)	–

今回はこの中でもθ=0°のときy=0になる理由を解説していきます。

tan0の計算

\(tan 0=0\)の理由だけならtan(タンジェント)定義から考えればOKです。

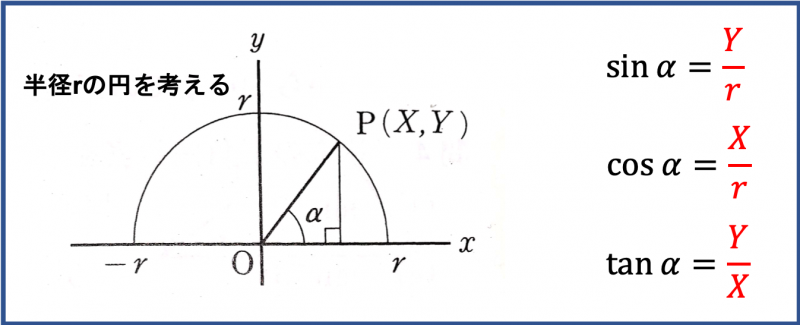
半径\(r\)の円があったとき、原点Oと円上の点P(X, Y)を結ぶ線とx軸がなす角をαとすると、
\(\tan α=\displaystyle \frac{Y}{X}\)となる。

ここで\(\displaystyle \lim_{α\to 0} \tan α\)とすると、
\(X= r\)で、\(Y=0\)となります。

つまり、\(\tan 0=\displaystyle \frac{0}{r}=0\)となります。

sin(サイン)とcos(コサイン)から解説

もう1つ、\(\tan\theta=\displaystyle \frac{\sin \theta}{\cos \theta}\)の公式から考えてみましょう。

\(\theta=0\)のとき、\(\sin\theta=0\)で\(\cos\theta=1\)です。
これを利用すると、\(\tan\theta\)も求めることが可能です。

\(\tan\theta=\displaystyle \frac{\sin \theta}{\cos \theta}=\displaystyle \frac{0}{1}=0\)

つまり、\(\tan 0=0\)となります。

tanθ=0になる他の角度

θ=0以外に\(\tan\theta=0\)になる\(\theta\)はあるのでしょうか。
これは\(y=\tan x\)のグラフを見ればわかります。

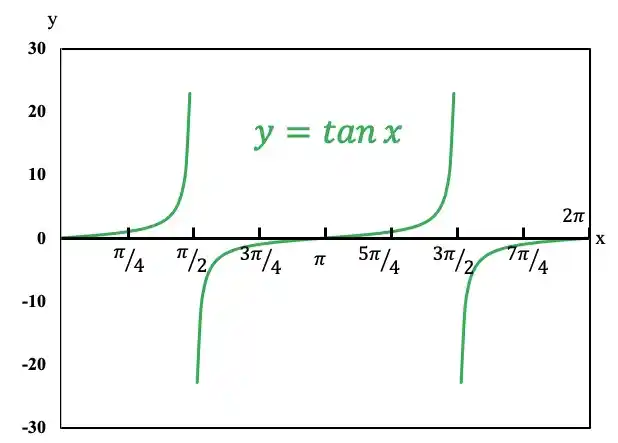
このグラフは横軸が弧度法で書かれていますが、
\(x=0,\ x=\pi(180°),\ x=2\pi(360°)\)で\(y=0\)になっています。

このように\(y=\tan x\)のグラフは\(180°\)ごとに同じ形を繰り返すので、
\(\tan \theta=0\)になる\(\theta\)は無数に存在します。

三角関数クイズ！

理解度チェックにご使用ください！

参考記事と1分の復習動画

こちらはグラフと弧度法の参考記事になります。

また今回の内容を1分で復習できる動画を作成しました。
良かったらご利用くださいませ。

今回は以上です！