今回は2次関数のグラフの書き方を解説します。
最大値・最小値の問題などでも必須の知識になるので、しっかり理解していきましょう。
前回は二次関数の頂点座標について解説しましたが、この知識はグラフを書く際にも絶対に必要です。
ですが、前回の解説を読んでいない方でも理解できるように、グラフの書き方を解説したので、よかったら最後まで読んでみてください。
この記事でわかること
- 二次関数の形が何で決まっているか
- 二次関数のグラフ①：頂点が原点にある場合
- 二次関数のグラフ②：頂点が原点ではない点にある場合
- グラフの平行移動のやり方
- グラフの対称移動のやり方
まずはグラフの書き方を理解して、平行移動と対称移動を理解していきましょう！
この記事を最後まで読めば、二次関数のグラフはバッチリです。しかも二次関数は重要単元なので、試験の点数も絶対に上がりますよ！一緒に頑張りましょう！
二次関数のグラフ：頂点が原点の場合
まずは中学校で最初に習う
$$y=ax^2$$
です。この形を使って二次関数の基礎を理解していきます。
この式を使う理由は『二次関数の頂点座標が原点に必ずあるから』です。
中学で習う二次関数でも解説しましたが、\(y=ax^2\)は特殊な二次関数です。
しかし、基本を習得するのに適した式なので、今回はこの式から学んでいきましょう。
グラフを書く手順
グラフを書くには、頂点座標がどこかを見つけて、頂点を基準にグラフを書く必要があります。
二次関数のグラフを書く手順
- 式から頂点を見つける
- 頂点を基準にグラフを書く
という２ステップでグラフを書くことになります。
では、ステップ１の頂点を見つけてみましょう！
式（\(y=ax^2\)）から頂点を見つける
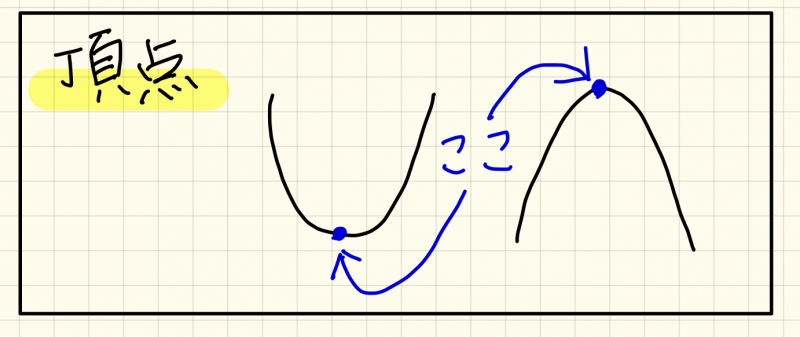
二次関数のグラフは絶対に「U」の字、もしくは「\(\cap\)」の字になります。
これの天辺が頂点となります。
\(y=ax^2\)の形では頂点は絶対に\((0,\ 0)\)です。
ですので、\(y=ax^2\)の\(a\)に何が入るかによってグラフの形が決定します。
例えば、\(a=1\)を入れて考えてみましょう。
\(y=x^2\)のグラフ
\(a=1\)だと上の画像のようなグラフになります。
また、\(a\)が\(1\)より大きくなれば、上のグラフより幅が狭くなります。
\(1\)より小さくなれば広くなります。
\(a\)が負の数なら逆さ向きになります。
二次関数グラフのポイント
- \(a\)が大きいと幅が小さくなる
- \(a\)が小さいと幅が大きくなる
- \(a\)が正なら上に凸、\(a\)が負なら下に凸
↓ もっと詳しい解説はこちらをチェック ↓
いくつか書いておくので参考にしてください。
ここから先は式の形が変わるけど、\(a\)の値によってグラフの形が決まるのは変わらないです！式の形によって変わるのは、原点の位置だけと覚えて次に進みましょう！
二次関数のグラフ：頂点が原点にない①
今度は\(y=ax^2-b\)の形を見ていきましょう！
この場合、頂点座標は\(b,\ 0\)となります。
と言ってもわからないと思うので、１つずつ解説していきます。
グラフを書く手順（復習）
グラフを書くまでの２ステップはなんでしたか？
- 式から頂点を見つける
- 頂点を基準にグラフを書く
ですね。ではまず頂点を見つけましょう。
\(y=a(x-b)^2\)の頂点を見つけよう
頂点の見つけ方は簡単です。
\(y=a(x-b)^2\)の\((x-b)^2\)の部分がゼロになるxを探せばいいだけ！
つまり、\(x-b=0\)になる\(x\)を見つければいいだけです。
\(x=b\)ですよね！\(x=b\)のとき、\(y=0\)なので、頂点座標は\((b,\ 0)\)となります。
「なんで、\(x-b=0\)になればいいの？」
と疑問に思った方はこの解説をチェックしてみましょう！
頂点が原点にあるときは\((0,\ 0)\)を頂点にしてグラフを書きました。
今回は\((b,\ 0)\)を頂点にしてグラフを書けばOK。
形は\(y=ax^2\)と同じです。
つまり、下の図のように頂点の位置が変わっただけで他には何も変わっていません！！
\(y=3(x-2)^2\)なら\((2,\ 0)\)を基準に、\(y=3x^2\)のグラフを書きましょう。
\(y=-(x-5)^2\)なら\((5,\ 0)\)を基準に、\(y=-x^2\)のグラフを書くだけです。
式の形は複雑になったけど、グラフにすると、そんなに変わってないことがわかりますね！
二次関数のグラフ：頂点が原点にない②
最後の式は\(y=a(x-b)^2+c\)です。
実はこの形が数学Iで習う基本的な形となります。
式の形を見ると、新しく「\(+c\)」が追加されましたね。
\(+c\)があることで、頂点座標が\((b,\ c)\)となります。
では実際に頂点を探してみましょう。
頂点座標を求める
ステップ１として、\(y=a(x-b)^2+c\)の中の\((x-b)^2\)が\(0\)となる\(x\)を探します。
つまり\(x=b\)ですね。\(y=a(x-b)^2\)の式ですと、頂点は(b, 0)となりました。しかし今回は「\(+c\)」が後ろについてます。
よって、\(y=a(x-b)^2+c\)で\(x=b\)のとき、\(y=c\)となります。
\(y=c\)になる計算
$$\begin{align}y &=a(x-b)^2+c \&=a(b-b)^2+c \&=0+c \&= c \end{align}$$
以上より、\(y=ax^2+bx+c\)の頂点は\((b,\ c)\)です。
あとは、\((b,\ c)\)の頂点を基準に、\(y=ax^2\)のグラフを書けばOKとなります。
\(y=3(x-2)^2+4\)なら\((2, 4)\)を基準に、\(y=3x^2\)のグラフを書きましょう。
\(y=-(x+5)^2-1\)なら\((-5, -1)\)を基準に、\(y=-x^2\)のグラフを書くだけです。
一旦まとめましょう。
頂点のまとめ
- \(y=ax^2\)⇨頂点は(0, 0)
- \(y=a(x-b)^2\)⇨頂点は(b, 0)
- \(y=a(x-b)^2+c\)⇨頂点は(b, c)
あとは、これらの頂点から二次関数を書けばいいだけです。例えば$$y=2(x-4)^2+3$$
の場合ですと、頂点は(4, 3)です。
なので、この頂点(4, 3)から\(y=2x^2\)のグラフを書けばいいだけです。
もう一つ見てみましょう。
$$y=\frac{1}{2}(x+3)^2-5$$
って式があったとします。
この場合の頂点はどこでしょうか。
頂点は(-3, -5)です。(3, -5)もしくは(3, 5)と思った方はいませんか？この辺の符号は私でもたまに間違えるので、注意が必要です。
頂点が分かったので、あとは(-3, -5)をスタートして\(\frac{1}{2}x^2\)のグラフを書くだけでOKです！
平行移動：二次関数グラフ
ここからはグラフの移動について解説していきます。
まずは平行移動です。
復習になりますが、二次関数の基本的な式は$$y=a(x-b)^2+c$$です。
この式は見た目ほど難しくありません！
グラフの平行移動の具体例
【例題】
\(y=2x^2\)をどのように移動すれば、\(y=2(x-3)^2+5\)のグラフとなるでしょう。
ヒントは、\(y=2x^2\)の頂点座標をどのように移動したら、\(y=2(x-3)^2+5\)の頂点座標になるかを考えるといいです。
解答は↓をタッチ！
【答え】
\(x\)方向に\(3\), \(y\)方向に\(5\)平行移動する。
【解説】
まずは、図を見てみましょう。
二次関数のグラフの平行移動では、頂点座標を基準に考えます。
\(y=2x^2\)の頂点座標は原点、つまり\((0,\ 0)\)ですね。
次に、\(y=2(x-3)^2+5\)の頂点座標は\((3,\ 5)\)です。
つまり、
$$(0,\ 0)\ \rightarrow\ (3,\ 5)$$
にすれば良いので、\(x\)軸は\(+3\)移動、\(y\)軸は\(+5\)移動すればOK
以上より、『\(x\)方向に\(3\), \(y\)方向に\(5\)平行移動する。』が答えとなります。
注意点があるとすればこの形。$$y=2(x+1)^2-1$$\((b=-1, c=-1)\)ですよね。
つまり、\(x\)方向に\(-1\)、\(y\)方向に\(-1\)移動するということです。
うっかり、「\(b=1\)だ！」と勘違いしないように気を付けましょう。
\(y=a(x-b)^2+c\)の平行移動は理解できましたか？まだ完璧じゃないと思います！でも基礎はバッチリできたので、あとは練習問題をたくさん解けば完璧になりますよ。
対称移動：二次関数グラフ
最後はグラフの対称移動について解説していきます。
対称移動は、\(x\)軸、\(y\)軸、原点の3種類に対しても対称移動があります。
対称移動３種類
- \(x\)軸に対称な移動
- \(y\)軸に対称な移動
- 原点に対称な移動
１つずつ見ていきましょう。
\(x\)軸に対称な移動
\(x\)軸に対称な移動は、\(x\)軸を鏡とした場合に映る点やグラフです。
図を見てみましょう。
\(x\)軸に対称な移動は、\(x\)軸に折り目をつけるとグラフが重なるイメージです。
\(y\)軸に対称な移動
\(y\)軸に対称な移動は、\(y\)軸を鏡とした場合に映る点やグラフのイメージになります。
図を見てみましょう。
\(y\)軸に対称な移動は、\(y\)軸で折り目をつけるとグラフが重なるイメージです。
原点に対称な移動
原点に対称な移動は、\(x\)軸に対称な移動と、\(y\)軸に対称な移動を合わせた移動です。
図を見てみましょう。
原点に対称な移動は、\(x\)軸で折り曲げて、\(y\)軸で折り曲げるとグラフが重なるイメージです。
原点に対称な移動は少しややこしいですね。
では移動した時の式はどうなるのか見ていきましょう。
対称移動の式の変化
結論から言うと、\(x\)軸に対称な移動は\(y=-y\)を代入し、\(y\)軸に対称な移動は\(x=-x\)を代入します。
原点に対称な移動の場合は\(y=-y,\ x=-x\)を両方代入すると対称移動の完了です。
二次関数｜対称移動の式変化
- \(x\)軸に対称移動\(\ \rightarrow\ \)\(y=-y\)を代入
- \(y\)軸に対称移動\(\ \rightarrow\ \)\(x=-x\)を代入
- 原点に対称移動\(\ \rightarrow\ \)\(y=-y\)と\(x=-x\)を代入
図を見るとわかりますが、例えば\(x\)軸に対称な移動だと、\(x\)座標は変わらずに\(y\)座標だけ反転しています。
なので、\(x\)軸に対称な移動だと\(y=-y\)になるのです。
対称移動の例題
例題を2問解いてみましょう。
【例題】
\(y=2x^2\)を\(x\)軸、\(y\)軸、原点に対称移動した時の式を答えなさい。
\(x\)軸：\(-y=2x^2\rightarrow\ y=-2x^2\)
\(y\)軸：\(y=2(-x)^2\rightarrow\ y=2x^2\)
原点：\(-y=2(-x)^2\rightarrow\ y=-2x^2\)
どこを対称に移動するとき、何を代入するかをしっかり理解しておけば簡単に解けるでしょう！
【例題２】
\(y=-(x-3)^2+4\)を\(x\)軸、\(y\)軸、原点に対称移動した時の式を答えなさい。
\(x\)軸：\(y=(x-3)^2-4\)
\begin{eqnarray}
-y &=& -(x-3)^2+4 \\
y &=& (x-3)^2-4 \end{eqnarray}
\(y\)軸：\(y=-(x+3)^2-4\)
原点：y = (x+3)^2-4
\begin{eqnarray} -y &=& -(-x-3)^2+4 \\
y&=& (x+3)^2-4 \end{eqnarray}
対称移動はややこしく感じるかもしれないけど、ポイントは２つだけだよ！『どこの軸に対称に動かすのか』と『その時に何を代入するのか』。計算自体は難しくないから、確実に理解しておくことをオススメします！
二次関数のグラフ｜まとめ
この記事で解説したこと
- 二次関数の形が何で決まっているか
- 二次関数のグラフ①：頂点が原点にある場合
- 二次関数のグラフ②：頂点が原点ではない点にある場合
- グラフの平行移動のやり方
- グラフの対称移動のやり方
グラフの書き方からグラフの移動まで解説してきました！
しっかり解説したので、一度では完璧に理解できていないかもしれません。しかし気にしなくてOKです。数学は何度も繰り返すことで、理解が深まっていく教科です。もう一度読みたい時のために、このページをブックマークしておきましょう！！
次回は最大値と最小値を求める解説です！
