今回のテーマは『空間図形』です。
解説する内容はこちら!
空間図形について解説していきます!空間図形は平面図形と違って、立体的な物を頭で動かす力が必要です。
立体的な図形を平面である紙や電子機器の画面上に書くからです。空間図形は頭の中で、立体を動かすことができるかが全てと言っても過言ではありません。
そこで、この記事では立体的な図形を3Dの図で書いて、なるべくイメージしやすい解説を心がけました。この記事を最後まで読むと空間図形は完璧に理解できます!
空間図形で悩むはずだった時間を、他の教科に回して全教科の得点アップを狙いましょう!
いろいろな立体
いろいろな立体を解説していきます。↓関連記事はこちら
解説する立体は、角柱・円柱・角錐・円錐・多面体の全部で5つです。
では柱・錐・多面体の3部に分けて解説していきます!
角柱と円柱
まずは角柱と円柱です。角柱と円柱は小学生で習う算数にも出てきたので、「知ってる!」って人も多いと思いますが、復習も兼ねて解説していきます!
角柱とは
角柱とは、『多角形を底面とする柱体』のことです。

底面とは柱を立てたときに底にくる面です。
つまり、角柱と一言で言っても、三角柱や五角柱、六角柱など様々な形があるわけです。
円柱とは
それでは円柱の解説をしていきます。
円柱とは、円を底面に持つ柱体のことです。

角柱とは違い、円は1種類なので形としては、この形しかありません。
半径と高さが変わって大きさが変わることは、もちろんありますよ。
角錐と円錐
次は角錐と円錐です。基本的に角柱・円柱と底の面(底面)は同じですが、上は1点しかないのが特徴です。
ピラミッドのイメージが近いかもしれません。
では、角錐から見ていきましょう。
角錐とは
角錐とは、「平面上のある多角形の頂点と、平面外の一点とを結んでできる立体のこと」です。
よくわかりませんね。図を使ってみていきましょう。

このように、三角形や四角形から1点に向かって伸びているのが、角錐です。
底の面を『底面』、横の面を『側面』と呼びます。
また、底面が三角形・四角形の角錐は、それぞれ三角錐・四角錐と呼ばれます。もちろん、五角錐や三十角錐なんかでもOKです。
中でも底面が正三角形や正方形で、側面が全て合同な三角形の角錐をそれぞれ『正三角錐』・『正四角錐』といいます。

円錐とは
円錐とは、「平面上のある円の円周と、平面外の一点とを結んでできる立体のこと」です。
簡単にいうと、角錐の底面が円になった図形です。

円錐には正円錐はなく、ただの円錐となります。
回転体とは
回転体とは、「平面図形をある直線を軸に1回転させてできる立体のこと」です。

回転体を回転の軸を含む平面で切ると、切り口の平面は軸に対して線対称な図形となります。

また、軸を含む平面で切れば、どこで切ったとしても切り口は合同な図形になります。
正多面体
多面体とは、「複数の平面に囲まれた立体のこと」です。
身近な例でいくと、サイコロやダイヤモンドなんかは多面体です。

多面体の中でも、正多面体という多面体が全部で5種類存在しています。
正多面体とは、「すべての面が合同な正多角形でできており、頂点に集まる面の数が全ての頂点で等しい多面体のこと」です。
正多面体は『正四面体』『正六面体』『正八面体』『正十二面体』『正二十面体』の5つしかありません。

ちなみに中学生だった僕は5つしかないと聞いて、「他にないのかな?」と探しましたが、僕は発見できませんでした!笑
次は平面や直線の位置関係です!
平面や直線の位置関係
平面や直線の位置関係の解説をしていきます!↓関連記事はこちら

解説する内容は、平面が決まる条件、直線と直線の位置関係、直線と平面の位置関係、平面と平面の位置関係の4つです。
では1つずつ見ていきましょう!
平面が決まる条件
平面が決まる条件とは、「この条件なら、この平面以外ありえないよね!」と言う条件のことです。
まずはイメージしてみましょう。何もない空間を思い描いてください。真っ白な音も匂いもない空間です。
そこに平面が現れました。四角形です。自由に動き回っています。

平面は空間では自由に動き回ることができる、どんな平面でも存在できるのです。
はい、戻ってきてください笑
では、平面のうち何が決まれば、平面の自由を奪って、「君はこの平面だよ!」と言えるのか。これが平面が決まる条件です。
平面が決まる4つの条件
平面が決まる条件は次の4つです。

この4条件のどれかを満たすと、平面は自由に動けなくなるのです。
「あれ?交わる2直線と平行な2直線があるなら、単に2直線を含む平面じゃダメなのかな?」
と質問を受けることがたまにあります。2直線があったら平行か交わるかの2つしか位置関係がないからです。
実は平面図形だとその2種類しかないのですが、空間図形になると、もう1つ位置関係が存在します。
それについては次に解説します。
直線と直線の位置関係
直線が2本あったとき、平面図形だと、2直線の位置関係は平行か交わるかの2つでした。
しかし空間図形だと、もう1つ『ねじれの位置』という位置関係が存在します。
交わりもしないし、平行でもない位置関係をねじれの位置といいます。

ねじれは受験でも出る重要なキーワードなので覚えておきましょう!
直線と平面の位置関係
直線と平面の位置関係にも、平行と垂直があります。
直線と平面の平行とは、「直線と平面が交わらないこと」です。
例えば、図のような直線ℓと平面Pは交わらないので、平行と言えます。

平行を表す記号は平面図形と同じです。
$$ℓ/\! /P$$
と書きます。
直線ℓと平面Pが1点で交わって、その点を通る平面P上の全ての点と垂直に交わるとき、直線ℓと平面Pは垂直であるといいます。
よくわからないと思うので、図でみてみましょう。

垂直も記号は変わらないので、下記のように表します。
$$ℓ\perp P$$
また、平面が決まる条件に、「交わる or 平行な2直線を含む」とあるので、直線ℓが平面P上の2本の直線と垂直であることを示せば、直線ℓと平面Pが垂直だと証明できます。
この辺りは難しいので、頭の片隅に置いておいて、練習問題などで出会ったら「なんかあったぞ!」くらいに引き出せるようにしておきましょう!
平面と平面の位置関係
最後は平面と平面の位置関係です。
2つの平面がPとQが交わらないとき、平面Pと平面Qは平行であるといい、\(P/\! /Q\)と表します。

2つの平面が交わるときは交線ができます。
交線とは、「2つの平面が交わるとき、交わっている直線のこと」です。
また、平面Pに垂直な直線ℓを平面Qが含むとき、平面Pと平面Qは垂直であるといい、\(P\perp Q\)と表します。

立体の体積
立体の体積について、公式と計算方法を解説していきます!↓関連記事はこちら

角柱と円柱の体積
角柱と円柱の体積の公式は同じです。
底面積を\(S\)、高さを\(h\)とすると、体積\(V\)は以下の公式になります。
$$V=Sh$$

これは小学生で習った角柱の体積を数学で表していますね。
算数では\(たて\times横\times高さ=体積\)と習いますが、底面積に高さを掛ければOKです。
やってる計算は同じですよ。
角錐と円錐の体積
角錐と円錐の体積も同じ公式です。
底面積を\(S\)、高さを\(h\)とすると、体積\(V\)は以下の公式になります。
$$V=\displaystyle \frac{1}{3}Sh$$

公式に\(\displaystyle \frac{1}{3}\)が付いている理由は、高校数学で積分を習うとわかります。
難しい計算なので、今は無理矢理\(\displaystyle \frac{1}{3}\)が付くと納得しましょう!
一応計算方法のリンクを貼っておくので、気になる方は参考にしてください!

球の体積
球の体積も計算には積分という難しい計算が必要なので、今回は公式を覚えてしまいましょう。
半径\(r\)の球の体積\(V\)は下記の式で表すことができます。
$$V=\displaystyle \frac{4}{3}\pi r^3$$

覚え方は「身の上に 心配 あーる 参上」です。
身の上に心配がある人の前にスーパーヒーローが現れるイメージですかね!笑

\ おすすめの参考書! /
立体の表面積
体積がわかったので、立体の表面積について解説していきます。↓関連記事

表面積=底面積+則面積
立体の表面積とは、底面積と側面積の和で計算します。
底面積とは、立体の1つの底面の面積のことです。
側面積とは、立体の側面全体の面積のことです。

表面積・底面積・側面積の意味がわかったら、実際の立体の公式はどうなるか見ていきましょう。
角柱と円柱の表面積
角柱と円柱の表面積は公式が同じです。
$$(表面積)=2\times(底面積)+(側面積)$$
となります。
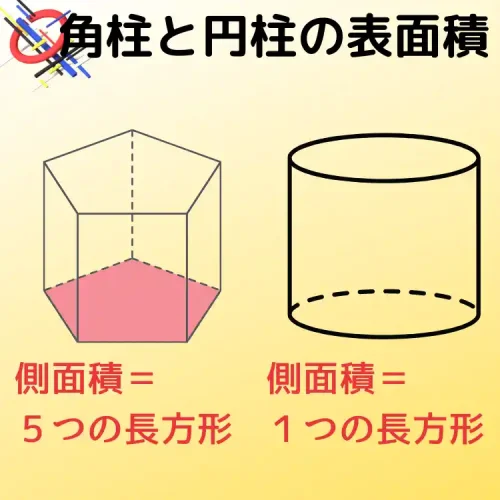
公式は同じですが、計算方法は異なります。
例えば五角柱の場合、側面積は四角形5つの面積の合計になります。
一方で円柱の場合、側面積は1つの長方形と見なすことができます。
(縦=高さ、横=円周の長さ)
なので、立体によって公式は同じでも、側面積の求め方が異なることは理解しておきましょう。
角錐と円錐の表面積
角錐と円錐も表面積を求める公式が同じです。
$$(表面積)=(底面積)+(側面積)$$
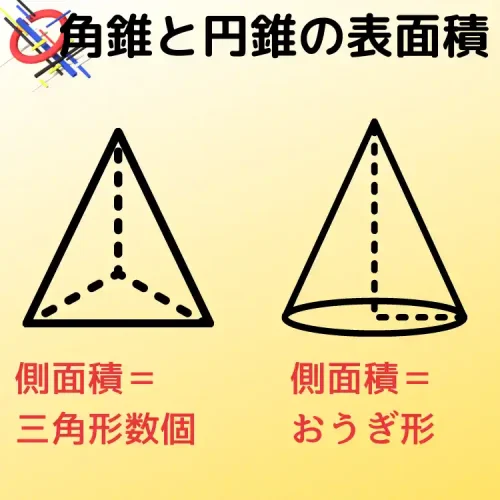
ただし、こちらも計算方法が異なります。
角錐の側面はいくつかの三角形なのに対して、円錐の側面は広げるとおうぎ形になります。
一問例題を解いてみましょう。

底面の円の半径が\(2cm\)なので、円周の長さは\(4\pi\)です。
側面のおうぎ形の弧の長さは、底面の円周の長さと等しいので\(4\pi\)です。
円錐を広げた時のおうぎ形の半径は\(3cm\)。
おうぎ形ではなく円だった場合、円周の長さは\(6\pi\)のはず。
ここから逆算すると、\(\displaystyle \frac{4\pi}{6\pi}\times360=240\)となり、中心角は\(240°\)とわかります。
よって、側面積は\(\pi \times r^2\times\displaystyle \frac{240}{360}=6\pi\ cm^2\)となる。
底面積は\(4\pi\ cm^2\)なので、表面積は\(10\pi\ cm^2\)となる。
球の表面積
最後の表面積は球の表面積です。
こちらも、計算で求めようとすると積分の知識が欠かせません。
なので、ここでは公式を暗記してしまいましょう。
半径\(r\)の球の表面積\(S\)は下記の通りです。
$$S=4\pi r^2$$

語呂合わせは「心配 ある 次女」です。
長女と三女は元気いっぱいで悩みがないのでしょうか?笑
今回は以上です!



コメント