\ 因数分解の計算機 /
中学生向けの因数分解の解説はこちらです!
因数分解とは
因数分解とは、展開とは逆で、式をかっこでくくって分解する計算方法です。
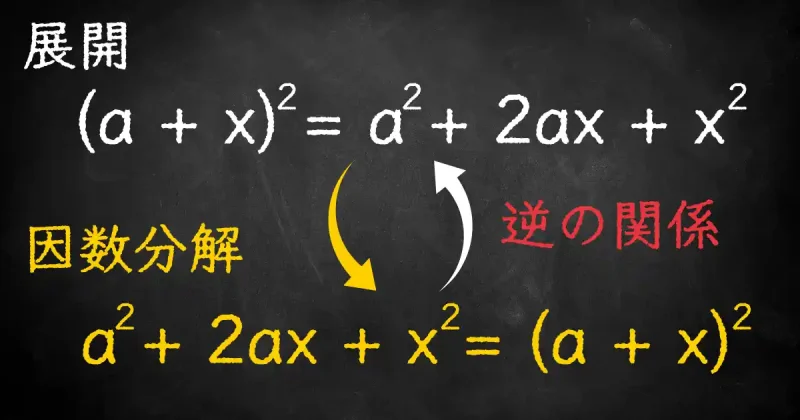
簡単に言うと、足し算と引き算で表していた式を、掛け算で表すのが因数分解です。
共通している文字や数字を取り出すのも因数分解と言います。
ではなぜ因数分解をするのでしょうか?
やり方や公式を説明する前に、因数分解する意味を確認しておきましょう。
因数分解はなぜ必要か
展開は計算しているけど、因数分解はもとに戻しているだけだよね?
なんで必要なの?
まずはこんな疑問にお答えしていきます。
勉強する理由がはっきりしている方が、モチベーションも上がると思います。
因数分解が必要な理由は、二次方程式 (三次方程式) を解くのに使うからです。
中学生で習う二次方程式や、大学入試で必要になる三次方程式は、数学の中でも難しい単元です。
そんな難しい単元をスラスラ解くために、因数分解が必要になります。
いま因数分解を理解すると、二次方程式の難しさが半減します!
みんながつまづく単元で自分だけスラスラ解けると思うと、やる気が出てきませんか?
では、ここから因数分解について解説していきます!
因数分解の公式一覧
1つ目は公式を使った因数分解です。
因数分解は半分以上、公式を知っているかどうかで決まります。
そのため最初は公式をしっかりと覚えていきましょう。
- 中学で習う公式
- 高校で習う公式
- 応用版の公式(大学入試向け)
の3つにわけて紹介しますね!
公式を一覧で見たい方は >>因数分解の公式一覧<< がオススメです。
二乗の公式(中学)
中学で習う2乗の公式は4つです。
この4つは必ず覚えてほしいくらい重要です。
しかし、4つも覚えられないよってときは、1番下の式だけ覚えましょう!
他の3つの公式は、1番下の公式から簡単に求めることができるからです。
例えば、\(a=y,\ b=y\)として、1番下の式に代入してみましょう。
\begin{eqnarray} & &x^2+(a+b)x+ab\\&=&x^2+(y+y)x+y\cdot y\\
&=&x^2+2xy+y^2\\&=& (x+y)^2 \\ \end{eqnarray}
一番上の式
(\(x^2+2xy+y^2= (x+y)^2\))
を求められました。
同様に(\(a=-y,\ b=-y\))とすると、上から2番目の式を求められます。
また、(\(a=y,\ b=-y\))とすると、上から3番目の式を求めることができます。
問題|二乗公式
4つの2乗公式を使って、実際に問題を解いてみましょう。
【問題】次の式を因数分解しなさい
\((1)\ a^2+6a+9\)
\((3) x^2-y^2\)
\((2)\ x^2-4x+4\)
\((4) x^2-6xy+8y\)
解答
\((1)\ a^2+6a+9\)
\(=a^2+2\times3a+3\times3\\=(a+3)^2\)
\((3) x^2-y^2\)
\(=(x+y)(x-y)\)
\((2)\ x^2-4x+4\)
\(=x^2-2\times2x+2\times2\\=(x-2)^2\)
\((4) x^2-6xy+8y^2\)
\(=x^2-(4+2)xy+4\times2y^2\\=(x-4y)(x-2y)\)
(1)と(2)は公式に当てはめてあげればOKです。
公式を使えるかの判断の基準として、2つのチェックポイントがあります。
- 次数が\(1\)の係数が偶数である。((1)の場合は\(6\)なのでOK)
- 定数項が整数の二乗である((1)は\(9\)なので\(3^2\)となりOK)
(3)は見た目で公式が使えるか判断できます。
(4)は、公式に当てはめてもOKですし、後ほど説明する『たすきがけ』という方法でも求めることができますよ。
次は3乗の公式をみていきます。
三乗の公式(高校)
これは4つとも覚えるのがオススメです。
4つ全部が難しければ、2番目と4番目を覚えましょう!
この2つの公式をベースに符号を変えれば、1番目と3番目の公式になりますよ。
では問題に移ります。
問題|三乗公式①
4つの3乗公式を使って、実際に問題を解いてみましょう。
【問題】次の式を因数分解しなさい
\((1)\ x^3+64\)
\((2)\ x^3-1\)
\((3) 8x^3+12x^2y+18xy^2+27y^3\)
\((4) x^3-9x^2y+81xy^2+729y^3\)
解答
\((1)\ x^3+64\)
\(=x^3+4^3\\=(x+4)(x^2-4x+16)\)
\((2)\ x^3-1\)
\(=x^3-1^3\\=(x-1)(x^2+x+1)\)
\((3) 8x^3+12x^2y+18xy^2+27y^3\)
\(=(2x)^3+(2x)^2\cdot (3y)+(2x)\cdot (3y)^2+(3y)^3\)
\(=(2x+3y)^3\)
\((4) x^3-9x^2y+81xy^2+729y^3\)
\(=(x)^3+(x)^2\cdot (9y)+(x)\cdot (9y)^2+(9y)^3\)
\(=(x+9y)^3\)
【応用】大学入試でよく出る公式
教科書に載っていることが少ない公式ですが、大学入試ではよく使われる公式を紹介します。
- \(a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)
難しければ飛ばしてOKです!
問題|三乗公式②
では、上記公式を使って1問だけ解いてみましょう。
【問題】次の式を因数分解せよ
\((1)\ x^3-y^3+8z^3+6xyz\)
解答
\((1)\ x^3-y^3+8z^3+6xyz\)
\(=x^3+(-y)^3+(2z)^3-3x(-y)(2z)\\=(x-y+2z)(x^2+y^2+4z^2+xy+2yz-2zx)\)
たすきがけのやり方とコツ
2つ目はたすきがけを使った因数分解です。
前章で合計で9つの公式を紹介しましたが、公式に当てはまらない因数分解もあります。
公式が使えないときは、『たすきがけ』と呼ばれる方法で因数分解をします。
ここではたすきがけのやり方を解説していきます。
図を書いて解くやり方
たすきがけは図を書いて計算するのが一般的です。
ここでは2つのステップにわけて、解き方を解説します。
- 二乗の項の係数と定数項に注目する
- 組み合わせを試してみる
この2ステップです。
ステップ1|2乗の項の係数と定数項に注目
例題を解きながらやってみましょう!
【例題】次の式を因数分解せよ
\(x^2-6x+8\)
このとき二乗の項の係数(例題なら\(x^2\)の係数なので\(1\))と、
定数項(例題なら\(8\))に注目します。
ここで、ある数とある数を掛け算して、注目している数になる組み合わせを探します。
\(1\)なら「\(1\)と\(1\)」、「\(-1\)と\(-1\)」の2パターンです。
\(8\)だと「\(2\)と\(4\)」、「\(8\)と\(1\)」の2パターンありますね。
正負まで考えると「\(-2\)と\(-4\)」、「\(-8\)と\(-1\)」の計4パターンになります。

ここから1つの組み合わせを選んで図を書きます。
ここでは「\(1\)と\(1\)」、「\(-2\)と\(-4\)」を選びました。
下の図のように、斜め同士でかけ算をすると、\(-2\)と\(-4\)になります。
この2つの数を足すと\(-6\)です。
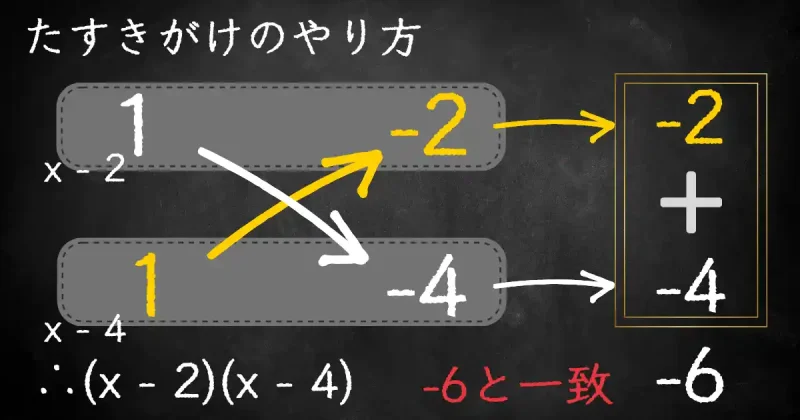
足した数の\(-6\)が次数\(1\)の係数と一致していればOKです。
(例題の場合は\(x\)の係数で\(-6\)なので一致)
この図より答えは\((x-2)(x-4)\)となります。
\(x^2-6x+8=(x-2)(x-4)\)
違う組み合わせを選んだ場合
もし正解の「\(1\)と\(1\)」、「\(-2\)と\(-4\)」ではない組み合わせを選んだら、どうしたらいいでしょうか?
例えば「\(1\)と\(1\)」、「\(1\)と\(8\)」を選んでいたら、たすきがけは下の図のようになりますね。
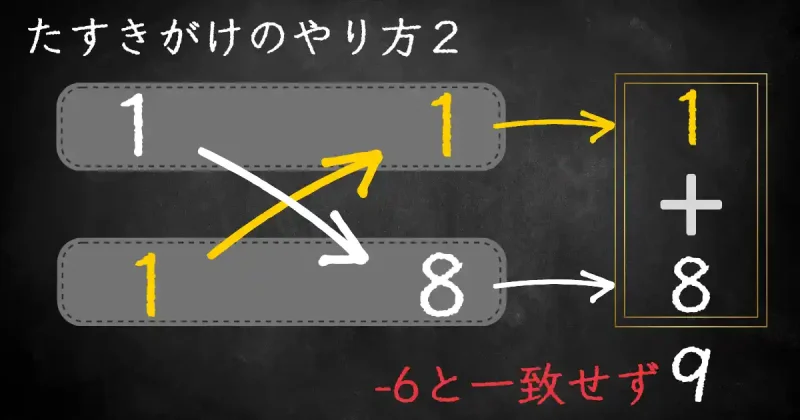
選んだ組み合わせが不正解だとわかったら、違う組み合わせを選んで、もう一度計算して正解を導きましょう。
慣れると簡単に正解の組み合わせを見つけることができます。
しかし慣れるまでが大変なので、たすきがけで正しい組み合わせを見つけるコツを紹介します。
たすきがけのコツ
たすきがけは練習すればするほど慣れるのが早くなります。
早く慣れるためにも、たすきがけのコツを知っておきましょう。
ダメだったら入れ替える
1つ目のコツは、「ダメだったら入れ替える」です。
\(3x^2+7x-6\)を因数分解するとします。
組み合わせは、
\(3\): 「\(3\)と\(1\)」、「\(-3\)と\(-1\)」
\(-6\): 「\(3\)と\(-2\)」、「\(-3\)と\(2\)」、「\(6\)と\(-1\)」、「\(-6\)と\(1\)」
です。
ここで、「\(3\)と\(1\)」「\(3\)と\(-2\)」を選んだとします。
答えを言うと選んだ組み合わせは正解です。

しかし、上下を逆に計算してしまうと不正解になります。
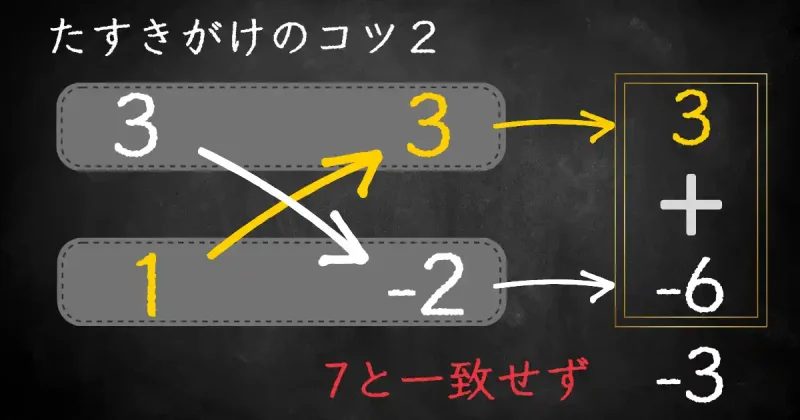
組み合わせは正しいのに不正解になったらもったいないですよね。
なので、1度上下を入れ替えて計算してみて、それでもダメなら組み合わせを変えるようにしましょう!
最初は時間を気にせず試してみる
2つ目のコツは「最初は時間を気にしない」です。
因数分解を習ってすぐは、たすきがけの計算にすごく時間がかかります。
でもそれでいいんです!!
時間を気にせず、1問1問と向き合えば、だんだんとたすきがけの計算が早く・正確になっていきます!
焦って次の問題をやると、逆に慣れるまでに時間がかかってしまうので注意ですよ!
たすきがけの練習
ではたすきがけの因数分解を4問ほど解いてみましょう。
たすきがけの問題
\((1)\ a^2+4a+3\)
\((3) 2x^2-5xy-3y^2\)
\((2)\ x^2-5x+6\)
\((4) 4x^2+13x-12\)
たすきがけの解答
\((1)\ a^2+4a+3\)
\(=a^2+(1+3)a+1\times3\\=(a+1)(a+3)\)
\((2)\ x^2-5x+6\)
\(=x^2+(1-6)x+1\times1(-6)\\=(x+1)(x-6)\)
\((3) 2x^2-5xy-3y^2\)
\(=1x\times 2x+(-6+1)xy+(-3y)\times y\\
=(x-3y)(2x+y)\)
\((4) 4x^2+13x-12\)
\(=x^2-(4+2)xy+4\times2y^2\\=(x-4y)(x-2y)\)
\ おすすめの参考書! /
共通因数でくくる因数分解
3つ目は共通因数をくくる因数分解を紹介します。
共通因数とは、式に共通して入っている数や文字のことです。
例えば、下記のような計算があります。
$$ax^2+2ax+a=a(x^2+2x+1)=a(x+1)^2$$
共通している\(a\)を外にくくり出してから、因数分解していますね。
このように、共通因数を外に出した後に、因数分解するやり方を解説していきます。
共通因数を外に出して、(1)公式で因数分解する問題と、(2)たすきがけで因数分解する問題を見ていきましょう。
くくった後に公式で因数分解する
共通因数くくり出しから、公式を使う因数分解は2ステップでできます。
- 共通因数でくくる
- 公式を使って因数分解する
です。
では問題を見ていきましょう。
問題|共通因数でくくる①
【問題】次の式を因数分解せよ
\((1)\ ax^2+4ax+4a\)
\((2)\ 5x^2-20y^2\)
解答
\((1)\ ax^2+4ax+4a\)
\(=a(x^2+4x+4)\\=a(x+2)^2\)
\((2)\ 5x^2-20y^2\)
\(=5(x^2-4y^2)\\=5(x+2y)(x-2y)\)
くくった後にたすきがけで因数分解する
共通因数くくり出しから、たすきがけを使ってやる因数分解は2ステップでできます。
- 共通因数をくくる
- たすきがけを使って因数分解する
です。
では問題を見ていきましょう。
問題|共通因数でくくる②
\((1)\ 2ax^2+6ax+4a\)
\((2)\ 5x^2-15xy-20y^2\)
解答
\((1)\ 2ax^2+6ax+4a\)
\(=2a(x^2+3x+2)\\=2a(x+2)(x+1)\)
\((2)\ 5x^2-15xy-20y^2\)
\(=5(x^2-3xy-4y^2)\\=5(x+y)(x-4y)\)
式を置き換える因数分解
4つ目は式を置き換える因数分解を紹介します。
レベルは少し高くなりますが、わかりやすく解説するので安心してください。
それでは例題を通して解説していきます。
式を文字に置き換える
簡単な例題からいきましょう。
【問題】次の式を因数分解せよ
\((a+b)^2+2(a+b)+1\)
【解答と解説】
このままだと因数分解できないので、
\((a+b)=X\)とおいてみます。
\((a+b)^2+2(a+b)+1=X^2+2X+1\)
となりますね。
これなら、二乗の公式を使えば因数分解できそうです。
\begin{eqnarray} & &(a+b)^2+2(a+b)+1\\&=&X^2+2X+1\\ &=& (X+1)^2 \\
&=&\{(a+b)+1\}\\
&=&(a+b+1)^2\end{eqnarray}
ポイント
\((a+b)=X\)とおいて因数分解し、最後に\(X=(a+b)\)に戻しましょう!
では練習していきます。
問題|式を置き換える①
\((1)\ (a+b)^2-2(a+b)-3\)
\((2)\ x^4+5x^2-6\)
解答
\((1)\ (a+b)^2-2(a+b)-3\)
\(a+b=X\)とおく
\(X^2-2X-3\\=(X+1)(X-3)\\=(a+b+1)(a+b-3)\)
\((2)\ x^4+5x^2-6\)
\(x^2=A\)とおく
\(A^2+5A-6\\=(A-1)(A+6)\\=(x^2-1)(x^2+6)\\=(x+1)(x-1)(x^2+6)\)
くくって置き換える
\(x\)や\(y\)でくくって置き換える因数分解もあるので紹介します。
これは少しレベルが上がるので、難しいと思ったら飛ばしてOKですよ!
因数分解は3ステップでできます。
- \(x\)の式になおす
- 定数項を因数分解して式を整理する
- 全体の式を因数分解する
ステップを見るだけでも複雑ですが、例題を使ってやり方を解説しますね。
【問題】次の式を因数分解せよ
\(x^2+2xy+y^2-x-y-2\)
【解答と解説】
こういった問題は、\(Ax^2+Bx+C\)の形に変形することを意識します。
\(x\)について整理すると、こうなります。
\begin{eqnarray}& & x^2+2xy+y^2-x-y-2\\
&=& x^2+(2y-1)x+(y^2-y-2) \\ \end{eqnarray}
ここで、
\(y^2-y-2=(y-2)(y+1)\)と因数分解できる。
\begin{eqnarray} &=&x^2+(2y-1)x+(y-2)(y+1)\\
&=&\{x+(y-2)\}\{x+(y+1)\}\\
&=&(x+y-2)(x+y+1) \end{eqnarray}
このように因数分解を何度もやる必要があります。
しかし、実際に手を動かして計算していれば、少しずつ慣れていくので心配しなくて大丈夫ですよ!
【応用】因数定理で因数分解するやり方
5つ目は応用編として『因数定理』を使うやり方を紹介します!
公式やたすきがけと比べると難しいです。
なるべく簡単に説明しますが、わからなければ飛ばしても大丈夫ですよ!
まずは因数定理とは何かについて簡単に説明して、因数分解のやり方、早く解くコツを解説していきます。
因数定理とは
因数定理
整式\(P(x)\)が\(x-a\)で割り切れるならば、\(P(a)=0\)である。
逆に、\(P(a)=0\)ならば、\(P(x)\)は\(x-a\)で割り切れる。
噛み砕いて説明します。
例えば、
\(P(x)=x^2-4\)だったとします。
\(x=2\)とすると、\(P(2)=4-4=0\)です。
これに因数定理を当てはめてみると、
『\(P(a)=0\)ならば、\(P(x)\)は\(x-a\)で割り切れる。』
と書いてあるので、\(P(x)=x^2-4\)は\(x-2\)で割り切れることになります。
実際、\(x^2-4\)を因数分解すると、
\((x+2)(x-2)\)ですよね。
つまり、\((x^2-4)\)を\((x-2)\)で割ると\((x+2)\)で割り切れていますよね。
この因数定理を使うことで、普通に計算するより簡単に、因数分解できる問題があります。
因数定理を使った因数分解を見ていきましょう。
因数定理で因数分解する
【問題】次の式を因数分解せよ
\(P(x)=x^3+5x^2-2x-24\)
ここで\(x=2\)とすると、
\(P(2)=2^3+5\cdot2^2-2\cdot2-24=8+20-4-24=0\)
となるため、因数定理より
\(P(x)\)は\(x-2\)で割り切れることがわかる。
整式の割り算より、
\((x^3+5x^2-2x-24)\div(x-2)=(x^2+7x+12)\)
たすきがけの因数分解を使うと、
\(x^2+7x+12=(x+4)(x+3)\)と因数分解できる。
以上より、\(x^3+5x^2-2x-24=(x-2)(x+4)(x+3)\)である。
因数の見つけ方|早く解くコツ
上記の計算で一番時間がかかるのが\(P(x)=0\)となる\(x\)を見つける作業です。
この\(x\)を因数と呼びますが、因数を見つける方法(コツ)を紹介していきます。
定数項の約数を見つける
まずは定数項の約数を考えましょう。
\(24\)の約数:\(1,\ 2,\ 3,\ 4,\ 6,\ 8,\ 12,\ 24\)
です。
この約数の正負(\(\pm\))のどれかを\(a\)としたら\(P(a)=0\)となります。
(※もちろん割り切れる\(x-a\)が存在しなければ\(P(a)=0\)にはなりません。)
代入する順番は絶対値が小さい方から順番にしていくのがオススメです。
(例:\(1,\ -1,\ 2,\ -2\cdots\))
\ おすすめの参考書! /
因数分解のまとめ
5種類の因数分解について解説してきました。
- 公式を使った因数分解
- たすきがけを使った因数分解
- 共通因数をくくる因数分解
- 式を置き換える因数分解
- 因数定理を使った因数分解
出てくる確率が高いのが、「公式を使った因数分解」と「たすきがけの因数分解」です。
逆に因数定理を使った因数分解は、使うことが少ないので、応用編と思って余裕があれば知識として取り入れましょう!
関連記事
まとめ記事
参考記事
[数1]整式とは?整式の整理と意味を解説
[数1]単項式とは?単項式の次数と係数、乗法、除法を解説
[数1]多項式とは?次数、項、係数、単項式や整式との違いを解説
[数1]単項式と多項式|単項式と多項式の違い、乗除の計算を解説
[数1]次数と係数の関係|単項式、多項式、定数項、同類項との関係
[数1]定数項とは?求め方、定数項の意味と多項式との関係を解説
[数1]同類項とは?多項式の同類項をまとめる問題、計算方法を解説
[数1]指数法則とは?分数、証明、問題を解説
分配法則とは?証明と問題、逆、分数、割り算を簡単に解説
[数1]展開公式|高校数学、公式一覧、3つ、4つ、三乗を紹介
[数1]因数分解とは?公式やたすきがけなど、5つのやり方を解説
因数分解公式一覧(高校数学)
たすきがけで解く因数分解の練習問題25問|難問あり!
絶対値とは?意味と計算を分かりやすく解説
不等式とは?方程式との違い、問題と解き方、計算方法と不等式の性質



コメント